$$\newcommand{\ket}[1]{\left|{#1}\right\rangle}\newcommand{\bra}[1]{\left\langle{#1}\right|}$$
2024 양자정보경진대회 복기본 (임의 양자상태 생성)
기간: 2024년 6월 21일 → 2024년 6월 23일
기본적으로 대회에서 구상할 때의 논리 순서대로 기술한 것이기에 각 과정에서 개연성이 부족할 수 있습니다. 여러가지 이유로 (당장 본인이 양자정보 잘 모르는 상태에서 대회 참여) 독자분이 필수적으로 있어야 한다고 생각되는 논의가 없거나 아예 틀린 내용이 있을 가능성이 높습니다. (예를 들면 상한만 구해놓고 하한은 안구한다던가...등등)
결과 : 대학원생 부문 2위 (근데 나빼고 다 학부생이었는데 대학원생부문이라니)
문제

풀이 과정
0.일반적인 \(N\) 에 대해서 어려운 이유
문제의 설명처럼, \(N=2^n\) 인 경우 구하는 상태의 파동함수는 다음과 같다.
$$
\ket{\psi_{2^r}} = \frac 1 {\sqrt {2^r}} \sum_{k=0}^{2^r-1} \ket{k}
$$
이 경우 우변이 \(\ket 0\) 의 Hadamard Transform, 즉 \(H_r \ket 0^{\otimes r}\) 이 되고 다음과 같이 정의된다.
$$
H_r = H_1 \otimes H_{r-1}
$$
여기서

$$
H_1 = \dfrac 1 {\sqrt 2} \begin{bmatrix} 1&1 \\
1&-1 \end{bmatrix}
$$
이므로 \(\ket 0^{\otimes r}\) 상태에 H gate \(r\) 개를 적용하면 구할 수 있다.
그러나 문제는 일반적인 경우를 요구하며, 이는 아래 식을 만족하는 operator를 찾고 구현하는 문제가 된다.
$$\frac 1 {\sqrt N} \sum_{k=0}^{N-1} \ket k = U \ket{0}^{\otimes r}, \quad 2^r \geq N
$$
이때 사용하는 conditioned gate들이 다른 큐비트 하나만을 체크한다면, 최소 \(\log_2 N\)개의 gate를 사용해야 하는데 이는 \(2^r\) 인 경우보다 항상 많다. 사용하는 gate수가 많아지면 연산 과정에서 발생하는 오류가 커지게 되어 원하는 상태를 만들기 어렵다.
1.개요
해당 식은 \(\ket{0}^{\otimes r}\) 에 적당한 rotation을 준 후 DFT를 적용한 것으로 해석할 수 있다. 그러나 DFT matrix는 아래와 같이 주어진다.
$$F_N = \begin{bmatrix} 1&1&1&\cdots &1\\
1&w&w^2&\cdots &w^{(N-1)}\\
1&w^2&w^4&\cdots&w^{2(N-1)}\\
\vdots&\vdots&\vdots&& \vdots \\
1&w^{2(N-1)}&w^{3(N-1)}&\cdots&w^{(N-1)^2}
\end{bmatrix}$$
모든 gate는 항상 \(2^n \times 2^n\) 행렬의 형태로 표현되어야 하나, 위의 행렬은 \(N \times N\) 행렬이므로 적당히 \( {\rm diag}( I_{2^r - N}, F_{N})\) 꼴의 연산자로 만들거나 \(F_{2^{r_k}}\) 꼴을 가지는 operator들의 tensorproduct 형태로 만들어주어야 한다.
우리는 원하는 연산자가 다음과 같은 형태를 가진다고 가정하고 주어진 \(N\) 에 해당하는 파라미터 \(m_k, \theta_k, p_k, q_k, n_k\) 를 구하려고 한다.
$$
U = R_{m_s}(\theta_{s}) {\rm diag}(I_{p_{s}} , F_{2^{n_s}} , I_{q_{s}} ) \cdots R_{m_1}(\theta_1){\rm diag}(I_{p_1} , F_{2^{n_1}} , I_{q_1} ) R_0(\theta_0)
$$
여기에서 \(n_k\)는 \(k\)번째로 적용되는 \(2^r\)-DFT 의 크기를 지정하며, \(p_k, q_k\) 는 각각 padding 을 위해 채워주는 단위행렬의 크기, \(m_k\) 는 \(k\)번째 \(R_Y\) gate가 작용하는 큐비트, \(\theta_k\)는 이때 회전되는 위상의 각도를 의미한다.
\(R_{m_k}\)가 한번에 여러 큐비트의 위상을 회전하는것은 상정하지 않았는데, 이는 \(n_k=0\) 으로 두면 표현될 수 있기 때문이다.
2.진폭 분배
아래와 같은 gate 조합이 주어졌다고 하자.

일반성을 잃지 않고 다음과 같이 가정할 수 있다.
$$
\ket{q_0} = \cos \theta_0 \ket 0 + \sin \theta_0 \ket 1\ket{q_1} = \ket 0
$$
이제 이 게이트를 통과한 다음의 상태를 구해보자. 먼저 \(\theta =-2 \cos^{-1}(\sin \theta_0)\) 로 두면 conditioned- \(R_Y\) gate를 통과한 상태는 다음과 같다.
$$
\ket{q_0q_1} = \cos \theta_0\ket{00} + \sin \theta_0( \sin \theta_0 \ket{10} + \cos \theta_0 \ket{11})
$$
이제 conditioned- \(H\) gate 까지 통과한 상태는 다음과 같다.
$$
\ket {q_0q_1} =\cos \theta_0 \ket{00} + \sin^2 \theta_0 \ket{10} +\frac 1 {\sqrt 2} \cos \theta_0 \sin \theta_0 \ket{11} + \frac 1 {\sqrt{2}} \cos \theta_0 \sin \theta_0 \ket{01}
$$
따라서 두 게이트를 모두 통과한 후, \(\ket {q_0}\)와 \(\ket{q_1}\) 가 \(1\)일 확률은 각각 다음과 같다.
$$
\begin{align*}
\ket {q_0}&:\sin^2 \theta_0 - \frac 1 2 \cos^2 \theta_0 \sin^2 \theta_0\ \ket{q_1}&:\frac 1 2 \cos^2 \theta_0 \sin^2 \theta_0
\end{align*}
$$
따라서 우리는 처음에 \(\ket{q_0}= R_Y(2\theta_0) \ket 0\)으로 두면 상태가 \(1\)일 확률을 \(\frac 1 2 \cos^2 \theta_0 \sin^2 \theta_0\) 만큼 \(\ket{q_1}\) 에 나누어줄 수 있다.
이때
$$
\tan\theta_1 = \dfrac{ \sin \theta_0 }{\sqrt{2+ 2\sin^2 \theta_0 \tan^2 \theta_0}}
$$
이다.
3.CNOT 게이트 개수
각 게이트의 구조는 다음과 같이 주어진다.

따라서 위의 조합으로 크기가 \(a+b\)인 진폭을 하나의 \(a\)와 \(p\)개의 \(b\)로 분배할때 \(2+p\)개의 cnot이 필요함을 알 수 있다. 또한 첫 번째 분배의 경우 초기화 과정에서 conditioned-\(R_Y\)를 생략할 수 있으므로 최종 cnot 개수에서 2를 빼줄 수 있다.
이제 \(n\)개의 동일한 상태를 만드는데 필요한 CNOT gate의 개수를 \(c_n\)이라 두면 다음이 성립한다.
$$
c_N \leq c_s + c_{N-s} + 3
$$
(이는 위의 예시에서 \(\theta_0 = \sin^{-1}\sqrt{s/N}\) 또는 \(\theta_0 = \cos^{-1}\sqrt{s/N}\) 로 두어 크기 \(1\)인 진폭을 \(s/N\)과 \((N-s)/N\)으로 나누어주는 상황과 같다.)
또한 \(2m\)의 경우 \(m\)에 대해 푼 후 하나의 비트를 추가하여 \(H\) gate를 씌우면 추가적인 cnot 없이 구현할 수 있으므로 \(c_{2m} = c_m\) 임을 알 수 있다. (따라서, \(0=c_1 = c_{2^k}\))
이제 최적의 분할 \(s : N-s\)를 찾아보자. 먼저 각각을 다음과 같이 이진법으로 나타내자.
$$
s = \sum_{i=1}^p 2^i u_i\
N - s = \sum_{j=1}^q 2^j v_j
$$
여기에서 \(u_i\)와 \(v_j\)는 이진법의 계수로 0 또는 1이다.
그러면 다음을 얻는다. 이 과정은 첫 번째 분할을 포함하지 않으므로 상한을 구할 때 \(2\)를 빼지 않는다.
$$
c_s \leq \sum_{i=1}^p c_{2^i u_i} + 3(p-1) \leq 4p -3 c_{N-s} \leq \sum_{i=1}^q c_{2^i v_i} + 3(q-1) \leq 4q -3
$$
따라서 대략적인 상한은 첫 번째 분할에서 사용하는 CNOT 1개를 포함해 다음과 같이 구해진다.
$$
c_N \leq (4p-3) + (4q -3)+1 = 4p+4q-5
$$
그런데 \(p \leq \lfloor \log_2 s \rfloor+1\) 이고, \(q \leq \lfloor \log_2 (N-s) \rfloor+1\) 이므로 다음을 얻는다.
$$
c_N \leq 4 (\lfloor \log_2(s)\rfloor +\lfloor \log_2(N-s) \rfloor )+3
$$
이 함수의 대략적인 개형은 아래와 같다.

따라서 \(N\)이 짝수가 아니면 \(s=1\) 또는 \(s=N-1\) 로 두는 것이 (\(\theta_0 =\cos^{-1}\sqrt{1/N}\) ) 최적일 것이라고 생각할 수 있다. 그런데 이 경우 분할 이후 각각 짝수개가 된다는 것을 알 수 있다.
다시 말해, 이진법으로 나타내었을 때 \(1\)로 표현되는 비트에 대해서만 '진폭 분할'을 해 주면 충분하다.
구체적인 방법 제시에 앞서 \(s=1\) 에 대한 CNOT gate 상한을 먼저 제시하겠다. 이진법을 이용하여 다음과 같이 표현하자.
$$
N = 2^{s_1} + 2^{s_2} + \cdots + 2^{s_r}
$$
그러면 다음과 같다.
$$
\begin{align}
c_N &= c_{2^{-s_1}N}\
&\leq c_{2^{-s_1}N-1 } + 1
\
&\leq c_{2^{-s_2(}2^{-s_1}N-1)-1 } + 1+3\
&\leq c_{2^{-s_{r-1} }(\cdots(2^{-s_1}N-1)\cdots )-1 } + 1+3(r-2)\
&=c_{2^{s_r}} + 1 + 3(r-2)\
&=3r-5
\end{align}
$$
4.구현
위의 방법을 종합하면 일반적인 \(N\)에 대해, 최대 \(3r-5\)개의 CNOT gate를 사용하는 알고리즘을 제시할 수 있다. 파이썬으로 작성한 코드는 아래와 같다. (IBM의 qiskit 사용)(다만 아래의 코드는 예외처리를 안해놔서 \(2^r\) 을 넣으면 제대로 동작하지 않음)
import numpy as np
from qiskit import QuantumCircuit
def uniform(M):
n = int(np.ceil(np.log2(M)))
q = QuantumCircuit(n)
l = []
for i in range(n):
if int(bin(M)[-i-1]):
l+=[i]
k = len(l)
for i in range(1,k):
q.x(l[i] )
Ms = [2**l[0]]
for m in range(1,k):
Ms+=[Ms[-1] + 2**l[m]]
Ms+=[0]
for i in range(l[0]):
q.h(i)
for m in range(k-1):
theta = -2*np.arccos( np.sqrt( 2**l[m] / (M - Ms[m-1])) )
if m == 0:
q.ry(theta , l[m+1])
else:
q.cry(theta , l[m], l[m+1] , ctrl_state = '0')
for i in range(l[m], l[m+1] ):
q.ch(l[m+1] , i , ctrl_state = '0')
q.measure_all()
display(q.draw("mpl"))
return q이를 이용해 제시된 \(N\)들에 대해 회로를 생성하고 실행하여 (이론적인) 진폭을 구하면 다음을 얻는다.
- N=3

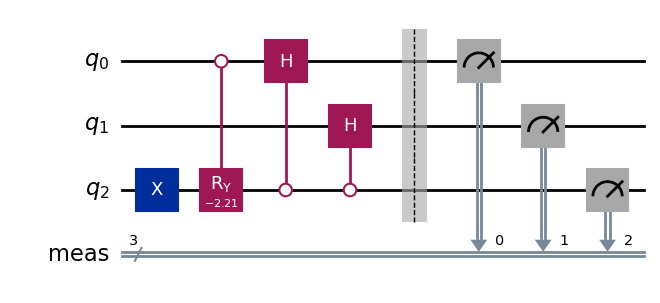
- N=5


- N=17


N=29


N=30


- N=31


5.QFT를 이용한 방법
QFT(Quantum DFT) 는 다음과 같이 구현된다.

import numpy as np
from qiskit import QuantumCircuit
def qft(n , q):
for i in range(n):
q.h(i)
for j in range(i+1, n ):
theta = 2*np.pi / 2**(j+1)
q.cp( theta , i , j, ctrl_state = '1')
q.measure_all()
display(q.draw("mpl"))
return qN=3 인 경우 QFT 회로 및 결과는 다음과 같다.


\(\ket{00}\) 과 \(\ket{01}\) 이 분리되지 않도록 \(q_1\)에 걸린 H gate를 conditioned로 바꾸어주면 된다.
\(N=5, 17\) 과 같이 \(N=2^r+1\) 인 경우 같은 방법으로 해결된다.
일반적인 경우에는, 결국 H gate 자체가 기저 2개에 대한 QFT로 해석할 수 있으므로, QFT 자체가 파동함수를 각 기저에 사영한 결과임을 이용할 수 있다. 원하지 않는 상태에 대해서는 사영된 결과가 0이 나오도록 QFT의 단계 사이에 \(R_Y\) gate를 삽입해 위상을 회전시켜 주면 문제를 해결할 수 있다.
이때, H gate가 가능한 상태의 경우의 수를 2개씩 늘려주므로 나누어주는 진폭의 비율은 2배씩 커진다. 따라서 \(R_Y\)의 각도 역시 이에 맞추어 조절해준다.
N=29 = 1 + 4 + 8 +16
import numpy as np from qiskit import QuantumCircuit q29 = QuantumCircuit(5) q29.h(0) q29.ry( 2*np.arccos(-np.sqrt(1/29)) , 0 ) q29.h(0) for i in range(1,5): if i < 3: q29.ch(0, i) elif i ==3 : q29.cry( 2*np.arccos(-np.sqrt(4/28)) , 0 , 3 ) q29.ch(3 , 0 , ctrl_state = '1') elif i == 4: q29.cry( 2*np.arccos(-np.sqrt(8/24)) , 3 , 4 ) q29.ch(4 , 3 , ctrl_state = '1') for j in range(i, 5 ): theta = 2*np.pi / 2**(j) q29.cp( theta , i-1 , j, ctrl_state = '1') q29.measure_all() display(q29.draw("mpl")) result = exe_qc(q29)
N= 30 = 2(1+2+4+8)
import numpy as np from qiskit import QuantumCircuit q30 = QuantumCircuit(5) q30.h(0) q30.ry( 2*np.arccos(-np.sqrt(1/15)) , 0 ) q30.h(0) for i in range(1,4): if i<2: q30.ch(0, i) elif i == 2: q30.cry( 2*np.arccos(-np.sqrt(2/14)) , 0 , 2 ) q30.ch(2 , 0 , ctrl_state = '1') elif i == 3: q30.cry( 2*np.arccos(-np.sqrt(4/12)) , 2,3 ) q30.ch( 3,2 , ctrl_state = '1') else: q30.h(i) for j in range(i, 4): theta = 2*np.pi / 2**(j) q30.cp( theta , i-1 , j, ctrl_state = '1') q30.h(4) q30.measure_all() display(q30.draw("mpl")) result = exe_qc(q30 , True , False)
N=31=1+2+4+8+16
import numpy as np from qiskit import QuantumCircuit q31 = QuantumCircuit(5) q31.h(0) q31.ry( 2*np.arccos(-np.sqrt(1/31)) , 0 ) q31.h(0) for i in range(1,5): if i<2: q31.ch(0, i) elif i == 2: q31.cry( 2*np.arccos(-np.sqrt(2/30)) , 0 , 2 ) q31.ch(2 , 0 , ctrl_state = '1') elif i == 3: q31.cry( 2*np.arccos(-np.sqrt(4/28)) , 2,3 ) q31.ch( 3,2 , ctrl_state = '1') elif i == 4: q31.cry( 2*np.arccos(-np.sqrt(8/24)) , 3,4 ) q31.ch( 4,3 , ctrl_state = '1') else: q31.h(i) for j in range(i, 5): theta = 2*np.pi / 2**(j+1) q31.cp( theta , i-1 , j, ctrl_state = '1') q31.measure_all() display(q31.draw("mpl")) result = exe_qc(q31 , True , False)